La ciencia ficción siempre ha fantaseado con la idea de viajar distancias imposibles utilizando instrumentos que alteren las propiedades del espacio a su alrededor. Este es el caso de la serie de videojuegos Portal, en la que el protagonista se vale del “Aperture Science Handheld Portal Device” para crear portales que conectan puntos del espacio de otra forma desconectados. Si bien en el juego se refieren a este tipo de estructuras como “portales”, su nombre real tanto en el mundo académico como en la cultura popular es el de “agujeros de gusano” desde que Charles Misner y John A. Wheeler acuñaran este término en 1957 (Misner and Wheeler). Aquí, se referían a los agujeros de gusano como puntos que conectarían regiones del espacio y del tiempo por medio de intensas deformaciones en el tejido espacio-temporal. Sin embargo, no fue hasta 2014 en la película Interstellar, cuando se le presentó al público una imagen de un agujero de gusano que pretendía ser exacta y acorde con las leyes físicas que conocemos hasta ahora (James et al.). Se debe aclarar, no obstante, que nunca se ha divisado un agujero de gusano debido tanto a las dificultades técnias que esto conllevaría (Dai and Stojkovic) como a la incertidumbre que existe actualmente en torno a su (no) existencia. La existencia de agujeros de gusano requeriría tanto la posibilidad de aparición de energía negativa como de curvas cerradas de tipo tiempo (es decir, de viajes en el tiempo) (Friedman and Higuchi). Además, de existir, muy probablemente este tipo de constructos se cerraría casi inmediatamente tras aparecer, por lo que la posibilidad de viajar a través de ellos sería limitada, más aún teniendo en cuenta que no sería un viaje cómodo debido a las intensas fuerzas de compresión y extensión a las que estaría sometido nuestro cuerpo al atravesar una región del espacio tiempo con una curvatura semejante. Aun con todo, ¿a quién no le produciría al menos una pizca de curiosidad el mirar a través de uno de ellos desde la comodidad de su sofá?

Las formas de representar un agujero de gusano son muy variadas, empezando por las más artísticas, pasando por modelos confeccionados con la ayuda de programas de CGI (Computer Generated Imagery) hasta las simulaciones más precisas como son las que podemos encontrar en Interstellar. En este post trataré de explicar cómo se puede conseguir replicar el agujero de gusano que aparece en la película Interstellar, e intentaré hacerlo sin mostrar ecuaciones ni código (ya están los papers y GitHub para eso) y partiendo de la base de la que partía yo cuando acometí este proyecto hace poco más de un mes: sin saber nada sobre el tema más allá de las ideas generales. Es importante recalcar la extrema complejidad de todo lo que voy a tratar aquí, por lo que simplificaré algunos detalles que no tendrán impacto en el conjunto, pero sí serán importantes a la hora de adquirir un conocimiento en profundidad de los temas que voy a tocar. En los siguientes apartados explicaré los fundamentos de la técnica de trazado de rayos (Ray Tracing) que utilizaremos para la simulación, cómo aplicarla al espacio curvo y los pasos que hay que seguir hasta dar con la imagen final. En la Figura 1 se muestra el resultado que he obtenido.

Agujero de gusano Figura 1: Imagen del agujero de gusano que se ha obtenido siguiendo el método que se describe en este post.

Tracemos unos rayos

Cuando miramos un objeto, ¿qué es lo que vemos? Esa es la pregunta fundamental que debemos hacernos antes de empezar con este proyecto, puesto que de su respuesta dependerá el enfoque que le demos. Cuando miramos un objeto nuestro cerebro está registrando la intensidad de luz que portan los rayos que inciden contra los receptores de nuestra retina. Estos rayos proceden de las fuentes de luz que tenemos en nuestro entorno y adquieren una intensidad u otra en función de los objetos contra los que impactan antes de llegar a la retina. Así, cuando estamos al aire libre y vemos una manzana de color rojo es porque algunos rayos procedentes del sol han chocado contra ella y ésta nos ha devuelto la parte roja de los mismos. Una cámara se vale de un principio muy similar para capturar una fotografía: en el cuerpo de la cámara se encuentra el sensor, organizado en píxeles formando una cuadrícula, y cada uno de estos píxeles registra la intensidad de la luz que lo atraviesa. Este mismo principio se aplica para generar imágenes por ordenador, se colocan en la escena los elementos principales (cámara, luces y objetos) y en un proceso denominado renderizado se traza la trayectoria de los rayos que impactan contra la cámara atendiendo además a sus rebotes y refracciones a los que éstos son sometidos. Esta técnica se denomina “Ray Tracing” y es fundamental en los procesos de renderizado modernos1 debido al realismo que ofrecen.

El trazado de rayos comienza colocando la cámara en un punto de la escena y ¿recuerdas que una cámara tiene un sensor que forma una cuadrícula y es ahí donde se proyecta la imagen? Utilizaremos este mismo concepto. A una distancia de la cámara (la llamaremos distancia focal) colocaremos el plano de la pantalla, como en la Figura 2. Será en este plano donde se formará la imagen. Parece evidente que no podemos saber a priori qué rayos llegarán a cada píxel de la pantalla, y trazar todos los rayos posibles desde la fuente de luz parece una estrategia abocada al fracaso puesto que la mayoría ni siquiera rozarán la pantalla. No obstante, podemos valernos de que el comportamiento de los rayos es determinista y trazarlos al revés, desde la cámara hacia la escena, haciéndolos rebotar con los objetos y hasta que confluyan en una fuente de luz o se pierdan en el infinito mar de rebotes y refracciones. Así, el concepto de cámara pasa a ser tan solo el punto desde el que parten todos los rayos. Con cada choque el valor de la intensidad del rayo de luz cambiará en función de los parámetros del objeto (no es lo mismo una bola de cristal transparente que un cubo de madera de color marrón). Es importante señalar que en escenas cotidianas estos rayos se moverán en línea recta entre choques, de ninguna forma curvarán sus trayectorias (así es como se comporta la luz, generalmente viaja en línea recta), por lo que será inmediato saber para cada momento de tiempo dónde se encuentra un rayo de luz. Este será uno de los puntos a tener en cuenta al introducir el agujero de gusano.

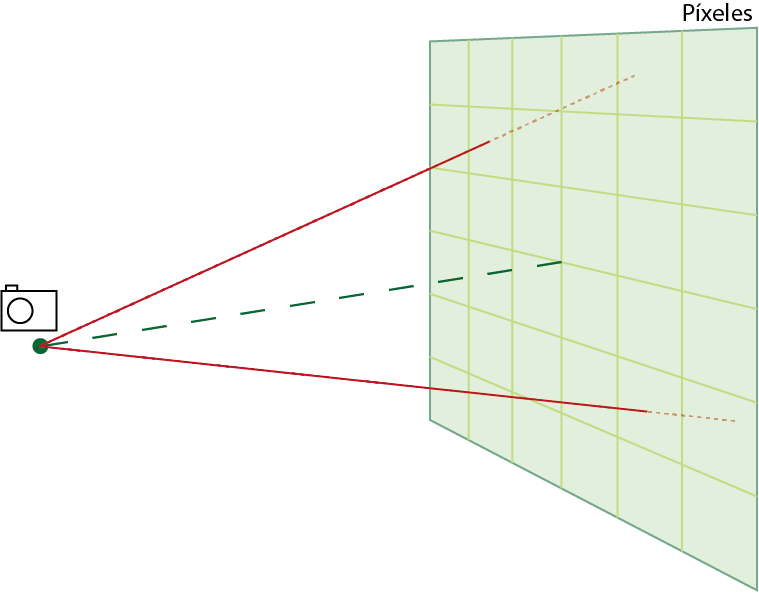Situación de la cámara Figura 2: Situación de la cámara y la pantalla.

No merece la pena entrar en el detalle de cómo calcular la dirección de un rayo después de un rebote ni su intensidad, pero dejo aquí un libro que me ha sido de mucha ayuda en mi todavía corto viaje por el Ray Tracing: Ray Tracing in One Weekend(Shirley).

Diseñando un agujero de gusano

Existen multitud de formas diferentes de diseñar un agujero de gusano tal que sea físicamente plausible2. La primera vez que se consiguió fue en 1973, cuando H. G. Ellis (Ellis) y K. A. Bronnikov (Bronnikov) (por separado) desarrollaron un modelo matemático del agujero de gusano tal y como lo conocemos ahora, en el que en principio podría existir traspaso de materia entre los dos lados del mismo. Este agujero en realidad atraía intensanmente a la materia hacia su garganta (el centro del agujero) por uno de sus extremos, mientras que la repulsión del otro extremo era igualmente intensa. Por este motivo, se le denominó Ellis drainhole (drain significa desagüe en inglés y hole es agujero).

Agujero de gusano de Ellis Figura 3: Agujero de gusano de Ellis. Imagen tomada de (James et al.).

Si bien en los años siguientes se desarrollaron otros agujeros de gusano con características variopintas (incluso algunos que permitirían viajar en el tiempo (Morris et al.)), debido a su simplicidad matemática trabajaremos con una versión ligeramente modificada del agujero de gusano de Ellis para generar nuestra imagen. ¿Por qué una versión modificada? La razón es muy sencilla: al parecer Christopher Nolan (el director de la película) quería tener control sobre la forma del agujero -el radio de la garganta y la distancia entre los extremos principalmente- y eso es algo que el agujero de gusano de Ellis no ofrece, así que desarrollaron una modificación para la película (James et al.). El estudio de animación que se encargó de todo esto se llama DNEG así que (oh, sorpresa) bautizaron a su agujero de gusano… Dneg.

Agujero de gusano Dneg Figura 4: Agujero de gusano Dneg. Imagen tomada de (James et al.).

Como parámetros para nuestro agujero utilizaremos un radio de la garganta (\( \rho \)) de 1km, una altura de la garganta (\( a \)) de 0.01km y situaremos la cámara a 6.25km de la boca superior del agujero, apuntando directamente a la boca del mismo. Como sabemos, se unirán dos partes diferentes del universo, cada una con su esfera celeste (sí, así se llama a la esfera alrededor del observador en la que se colocan los astros), así que la cámara estará rodeada por un cielo estrellado y apuntará hacia el planeta Saturno, que se encontrará al otro lado del agujero3. Las imágenes están disponibles en el material suplementario del paper original. Para imaginarlo -aunque no sea físicamente correcto-, podemos pensar en el agujero de la figura anterior con una esfera hueca a cada lado de la garganta en cuyo interior pegaremos una imagen con el contenido de esa porción del universo, esas serán las dos esferas celestes. Con esto ya tenemos todos los ingredientes necesarios para empezar a tomar nuestra foto.

Agárrate, que vienen curvas

Ya hemos visto cómo tratar con los rayos que se mueven por el espacio plano al que estamos acostumbrados (espacio euclídeo). Sin embargo, la propia definición de agujero de gusano implica una deformación del espacio, curvándolo y afectando a todos los objetos que se encuentran a su alrededor, incluidos los rayos de luz. Por este motivo, la trayectoria de los rayos cambiará en función de cómo deforme el espacio el agujero de gusano que diseñemos. No parece necesario ahondar en las ecuaciones porque explicarlas llevaría demasiado tiempo, tan solo es necesario saber que para cada momento en el tiempo podremos obtener la posición exacta en la que se encuentra el rayo. Para el lector interesado, las ecuaciones se encuentran en el apéndice de (James et al.). Resolveremos las ecuaciones numéricamente y con ello obtendremos de qué lado del agujero proviene el rayo y en qué punto de la esfera celeste correspondiente. Como hemos visto en el apartado anterior, cada esfera celeste es en realidad una imagen, así que tan solo tendremos que tomar el valor de la imagen en el punto donde ha chocado el rayo, de esta forma tendremos un mapeo entre los píxeles de la cámara (punto inicial de los rayos) y los píxeles de las esferas celestes (punto final de los rayos). En la siguiente figura se muestra una representación ficticia de este proceso para una de las dos esferas celestes.

Esfera celeste Figura 5: Mapeo de la esfera celeste a los píxeles de la pantalla. La representación es ficticia porque se está utilizando un espacio plano, entre la esfera celeste y la pantalla debería estar el agujero de gusano, por lo que las líneas no viajarían en línea recta.

Una vez obtenida la imagen podemos pasar a examinarla (Figura 1): vemos que la parte central se corresponde con la esfera celeste que hay en la parte del universo donde no está situada la cámara (Saturno), mientras que la parte externa es un cielo estrellado. Esto se debe precisamente a la curvatura del espacio. Como los rayos no viajan en línea recta, los píxeles del sensor de la cámara reciben luz desde ambos extremos, por lo que puede ocurrir (y de hecho ocurre) que dos píxeles contiguos reciban luz desde partes muy separadas del universo, de ahí que podamos ver los dos extremos de la boca del agujero a la vez. Vemos también en la imagen que el cielo estrellado alrededor del agujero ha dejado de ser “estrellado” para ser un amasijo de líneas curvas. Este efecto tiene su origen en la distorsion que el agujero crea en el espacio a su alrededor. Actúa como lente gravitacional, lo que implica hacer visible la luz que proviene de zonas que no deberían ser visibles si no hubiera agujero.

Otro efecto muy interesante es el que se crea en el límite de la boca del agujero de gusano: en el extremo opuesto a donde está Saturno se puede ver una imagen secundaria de él (al menos una región mínima con píxeles marrones). La imagen primaria de Saturno aparece gracias a los rayos que viajan directamente desde el planeta hasta la cámara. Las secundarias (hay más pero no son visibles) provienen de rayos que han recorrido caminos más largos por el agujero de gusano. Este efecto aparece también en agujeros negros y es bien conocido (Tsukamoto et al.). Además, como depende de los rayos que han recorrido un camino más largo hasta llegar a la cámara, su presencia depende de la longitud del agujero. En la siguiente figura se puede observar este fenómeno en un agujero con una longitud 100 veces mayor, con lo que se ve claramente la segunda imagen de Saturno. Se ha modificado también la curvatura de la boca del agujero al obtener esa imagen, provocando que la deformación en el espacio circundante sea también mayor.

Agujero de gusano modificado Figura 6: Imagen de un agujero de gusano Dneg. El aumento de la curvatura y la longitud de la garganta ocasionan una deformación todavía mayor del espacio alrededor.

Con esto concluyo esta entrada en la que he tratado de explicar cómo generar una imagen de un agujero de gusano utilizando tan solo las ecuaciones que lo gobiernan y una técnica muy conocida como lo es la de trazado de rayos. He querido transmitir en todo momento que este tema es extraordinariamente complejo y, por supuesto, hay detalles que he pasado por alto por miedo a que se volviera más denso si cabe.

El código que he escrito para generar todas las imágenes está disponible públicamente en un repositorio de GitHub. No está tan ordenado como me gustaría, pero era la primera vez que utilizaba C++/C en muchos años. Cualquier duda o comentario es bien recibida.

  1. Misner, Charles W., and John A. Wheeler. “Classical Physics as Geometry.” Annals of Physics, vol. 2, no. 6, Academic Press, December 1957, pp. 525–603, doi:10.1016/0003-4916(57)90049-0.
  2. James, Oliver, et al. “Visualizing Interstellar’s Wormhole.” Citation: American Journal of Physics, vol. 83, 2015, p. 486, doi:10.1119/1.4916949.
  3. Dai, De Chang, and Dejan Stojkovic. “Observing a Wormhole.” Physical Review D, vol. 100, no. 8, American Physical Society, October 2019, p. 083513, doi:10.1103/PhysRevD.100.083513.
  4. Friedman, John L., and Atsushi Higuchi. Topological Censorship and Chronology Protection. 2008.
  5. Shirley, Peter. Ray Tracing in One Weekend. 2020, https://raytracing.github.io/books/RayTracingInOneWeekend.html.
  6. Ellis, Homer G. “Ether Flow through a Drainhole: A Particle Model in General Relativity.” Journal of Mathematical Physics, vol. 14, no. 1, American Institute of PhysicsAIP, January 1973, pp. 104–18, doi:10.1063/1.1666161.
  7. Bronnikov, K. A. “Scalar-Tensor Theory and Scalar Charge.” Acta Phys.Polon.B, vol. 4, 1973, pp. 251–66.
  8. Morris, Michael S., et al. “Wormholes, Time Machines, and the Weak Energy Condition.” Physical Review Letters, vol. 61, no. 13, 1988, pp. 1446–49, doi:10.1103/PhysRevLett.61.1446.
  9. Tsukamoto, Naoki, et al. Can We Distinguish between Black Holes and Wormholes by Their Einstein-Ring Systems? 2012.

  1. La técnica de Ray Tracing no es la única actualmente pero sí una de las más utilizadas porque ofrece una buena relación entre la calidad final de las imágenes y el tiempo empleado para renderizar. ↩

  2. Que un agujero de gusano sea físicamente plausible implica que es una solución de las ecuaciones de Einstein, no que haya sido observado. ↩

  3. Se ha prescindido de colocar la cámara en la Figura 3 porque ésta es una representación del agujero en menos dimensiones de las que en realidad toman parte. Está bien para hacerse una idea de cara a la programación colocar la cámara mentalmente en la vertical de la garganta del agujero, apuntando perpendicularmente hacia ésta. Sin embargo, en dicha Figura en realidad se está representando el espacio-tiempo en sí, y todos los objetos deben estar sobre la retícula, incluida la cámara. ↩