La pregunta que encabeza este post es recurrente en todos los círculos de la Inteligencia Artificial. Aquellos que trabajan en NLP (procesamiento de lenguaje natural por sus siglas en inglés) buscan concebir sistemas que sean capaces de entender -procesar- lenguaje producido por seres humanos y tomar acciones acordes. GPT-3 es un ejemplo de esto, el cometido de este modelo tan solo es predecir (aunque muy acertadamente) la palabra más probable que seguirá una secuencia de texto (Brown et al.). Sin embargo, por cómo ha sido entrenado, en ningún caso se puede defender que el modelo posea una comprensión profunda de las palabras que está produciendo ni que tenga un objetivo en particular al expresarlas. Si se me permite mi opinión, creo que el salto que nos queda por delante hasta cubrir este último punto es todavía enorme y no vendrá en los próximos años. Al fin y al cabo, todavía no entendemos cómo funciona la mente humana. Así que la respuesta a la pregunta del encabezado será… “depende”, depende de a lo que nos refiramos con la palabra idioma.

Es por tanto relevante saber a qué nos referimos con “idioma” o “lenguaje” cuando hablemos de ello en este post. Nos estaremos refiriendo a un lenguaje común que compartan varios sistemas a través del cual puedan llegar a entenderse y transmitir ideas. No obstante, estas ideas vendrán predefinidas por un agente externo a la IA. Un ejemplo básico podría ser transmitir un número aleatorio de 0 a 9 del sistema A al B en un lenguaje común, que el B lo procesara, calculara su doble, lo devolviera a A y A interpretara el resultado correcto. En este post intentaremos sentar las bases de un proyecto que cumpla todos esos requisitos y una condición más: que el idioma que compartan ambos sistemas sea similar al del droide R2-D2 de Star Wars.

Dos no hablan si uno no quiere

Efectivamente, para que exista comunicación debe haber al menos dos sistemas: un emisor de información (transmisor) y otro receptor de la misma. Siguiendo la Teoría de la Comunicación de Claude E. Shannon (Shannon), es necesario además una fuente de información, un canal, un mensaje, un destinatario y un elemento de ruido. Si bien la definición precisa de estos componentes se deja a discreción del lector, es de capital importancia para este proyecto distinguir entre fuente de información y transmisor, y destinatario y receptor: cuando hablamos de transmisor nos referimos al sistema técnico encargado de codificar la fuente de información a un conjunto de señales aptas para el canal (y viceversa para el receptor, que la decodifica para que el destinatario pueda utilizar la información). Aplicado a la comunicación verbal entre dos personas A y B, la fuente de información será la idea de A, cuyo cerebro se encargará de codificar en forma de palabras -mensaje- que se enviarán por el aire -canal- hasta llegar a B. El cerebro de B decodificará las palabras y generará una idea, que en el mejor de los casos será igual a la idea del cerebro de A.

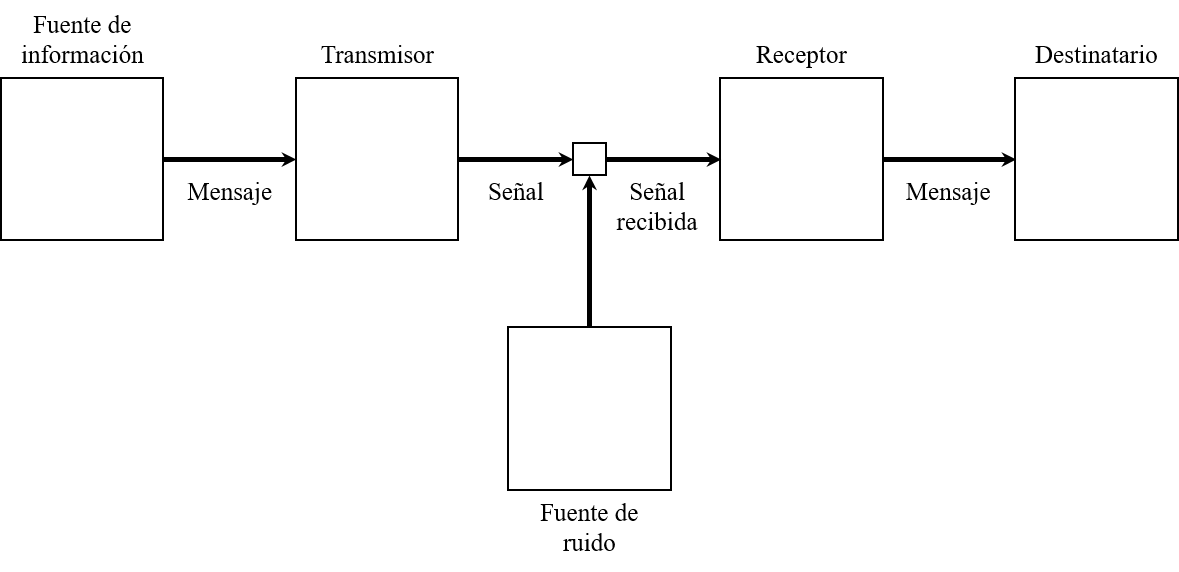Information theory Figura 1: Diagrama de la teoría de la información de Shannon. Adaptado de (Shannon).

Transformemos ahora esta teoría al campo de la IA. Como sabemos, las redes neuronales son tremendamente eficaces a la hora de generar representaciones a partir de datos, por lo que podríamos enfrentar dos de ellas (sujetos A y B) y hacerlas compartir mensajes. A codificaría el mensaje y B lo… ¿decodificaría? ¿Y qué pasaría si B quisiera transmitir una idea a A? Para encontrar la solución a esta pregunta podemos fijarnos en el sistema más eficiente que conocemos a la hora de producir y procesar lenguaje: el cerebro. Este órgano se encarga de ambas funciones simultáneamente (¿o es que no puedes escuchar música y hablar a la vez?), y eso se debe a que el flujo de información transcurre por zonas separadas1. Estas dos zonas son el área de Wernicke y el área de Broca, que se encargan de la comprensión y de la producción del lenguaje respectivamente (Neil). Siguiendo este ejemplo, parece lógico hacer que nuestros sujetos estén formados por dos redes diferentes y desconectadas. Una de estas redes, el encoder se encargará de producir el lenguaje mientras que el decoder tratará de comprenderlo. En caso de que A quiera transmitir una idea a B, será el encoder de A el responsable de transformar esta idea a un lenguaje común y el decoder de B lo interpretará.

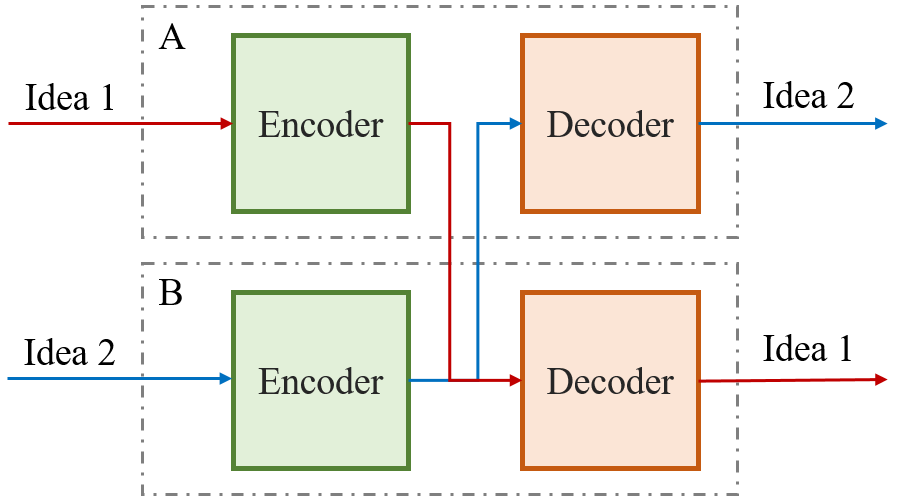Estructura Figura 2: Estructura de un sistema con dos individuos.

Hablemos tan claro como R2-D2

Describiré en primer lugar la forma de comunicarse de R2-D2 para aquellos que la desconozcan. Se trata de una serie de pitidos, silbidos y otros sonidos aglutinados para formar algo que se asemeja a frases (Bray et al.). En YouTube hay infinidad de vídeos mostrando estos sonidos. Intentaremos hacer que las redes neuronales imiten este lenguaje a la hora de hablar, forzando que la representación de la idea por parte del encoder sea también una serie de pitidos. Sin embargo, forzar este tipo de representación no es trivial por dos motivos: en primer lugar, el lenguaje debe ser creado espontáneamente a través de la conversación entre las redes, no debe existir ningún tipo de interacción humana en este proceso. En segundo lugar, debemos definir a qué nos referimos con “representación” en este contexto puesto que el lenguaje es muy variado. Abordaremos primero la segunda cuestión, lo que nos llevará inexorablemente hasta la solución de la primera.

Un sonido puede ser representado de tres formas diferentes en función de lo que busquemos conocer acerca del mismo:

  • Representación temporal: muestra la intensidad del sonido en función del tiempo.
  • Representación en frecuencias: explicado muy brevemente, todo sonido, por el hecho de ser una onda en función del tiempo, puede ser descompuesto en ondas más básicas con diferentes frecuencias. El método con el que pasamos de una onda en el dominio temporal a una onda en el dominio de frecuencias recibe el nombre de transformada de Fourier. La representación en frecuencias contiene información de lo importante (amplitud) que es cada frecuencia para dar lugar al sonido subyacente.
  • Representación en forma de espectrograma: las dos representaciones anteriores tienen dos dimensiones, i.e. amplitud en función del tiempo o amplitud de cada frecuencia. Sin embargo, podemos unir ambas para dar lugar a una representación tridimensional: tiempo, amplitud y frecuencia. Un espectrograma muestra la evolución de la frecuencia y de la intensidad en el tiempo. Típicamente, la intensidad se define por el color, mientras que el tiempo toma el eje de abscisas y la frecuencia, el de ordenadas. A diferencia de en los casos anteriores, un espectrograma puede ser guardado en forma de imagen ya que la informaciónm relevante está codificada tanto en el color de los píxeles como en su posición. La siguiente figura muestra el espectrograma de un fragmento de la voz de R2-D22.

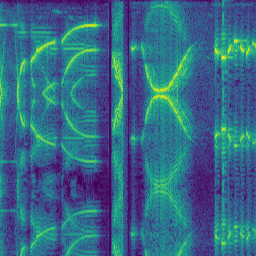Espectrograma Figura 3: Espectrograma de un sonido producido por R2-D2. Se ha calculado tomando la transformada de Fourier de todo el audio del vídeo en https://www.youtube.com/watch?v=2-BKjnAgNgY y dividiendo el resultado en imágenes de 256 píxeles.

Se ha demostrado que las redes neuronales operan bien con datos tabulados y especialmente bien con imágenes (Krizhevsky et al.)(He et al.), así que parece lógico utilizar el espectograma para esta tarea. En general, para trabajar con imágenes se utilizan redes neuronales convolucionales porque son capaces de capturar relaciones en ellas, normalmente a través de la identificación de bordes en diferentes direcciones y otras características más vagas como las texturas. Explicar en detalle cómo funcionan este tipo de redes daría para otro artículo, por lo que se deja al lector interesado el familiarizarse con este tipo de arquitecturas, ya que existen multitud de recursos disponibles ((Dot CSV), (Stanford) [en inglés], por ejemplo). Tan solo diré aquí que con una red de capas convolucionales podemos obtener una representación en varias dimensiones de los datos de entrada (una imagen). Es decir, podemos conseguir la traducción de un número cualquiera en una imagen, y esta traducción puede ser aprendida para una tarea concreta.

Un poco de arquitectura

Una vez abordados todos los aspectos técnicos del problema nos centraremos en definir la arquitectura del sistema y la forma de entrenamiento. Determinar la arquitectura de las redes generalmente tiene más de arte que de ciencia, por lo que no me explayaré en los detalles. En primer lugar, codificaremos la idea (el número) de forma One-Hot, lo que significa que para transmitir un dígito de entre \( N \) posibles utilizaremos un vector de \( N \) componentes con cero en todas ellas y un uno en la componente relevante. Por ejemplo, el vector para el número 1 en el intervalo \( [0, 4] \) será \([0, 1, 0, 0, 0]\). Para utilizar estos datos con redes convolucionales deberemos transformarlos a tres dimensiones \( (C\times H\times W ) \), aumentando en primer lugar la cantidad de componentes con al menos una capa fully connected y redimensionando el resultado. Posteriormente, añadiremos capas convolucionales de forma que el resultado sea un mapa de las dimensiones del espectrograma que buscamos. Como la tarea que buscamos resolver es simétrica (el encoder y el decoder deben realizar tareas opuestas), optaremos por arquitecturas simétricas para estas dos redes. Si hemos dicho que el encoder empezará con una capa fully connected seguida de capas convolucionales, el decoder empezará por capas convolucionales y por último otra fully connected. De esta forma, el diagrama anterior adquiere la siguiente estructura:

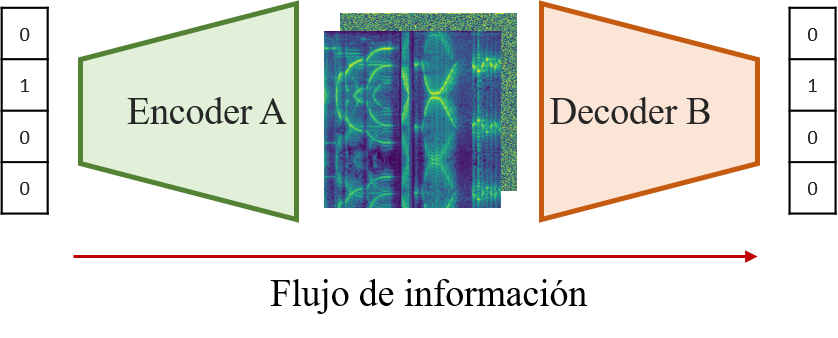Estructura con espectrograma Figura 3: Estructura de un sistema con dos individuos en el que se envía el número 1. Por comparación con la teoría de la información de Shannon, el espectrograma central muestra el mensaje. Solo se muestra una parte del sistema (conexión de A con B) por simplicidad.

Para hacer que un sistema de redes neuronales se comporte de una forma determinada se debe especificar una cantidad a minimizar. A esta cantidad se le llama loss, y en muchos casos es una función que depende de la salida de la red y de los datos originales3. Aplicado a nuestro problema, podemos definir inmediatamente una cantidad que el sistema debe minimizar: queremos que B interprete la misma idea que está intentando transmitir A. Como solo hay un número correcto cada vez, el problema es multiclase (predecir un número y solo uno de entre diez posibles) y minimizaremos la Cross-Entropy loss, definida como: \[ L_{CE} = - \sum_i^C t_i \log(s_i),\] donde \( C \) son las clases posibles y \( t_i \) y \( s_i \) representan la etiqueta real y la predicha por la red respectivamente (Gómez).

Minimizando la Cross-Entropy loss conseguimos que las dos redes se pongan de acuerdo en el número que están transmitiendo. Es importante puntualizar que tan solo minimizando esta cantidad las redes ya crearían un lenguaje interno a la salida del encoder, pero éste sería probablemente aleatorio. Como queremos que utilicen la voz de R2-D2, tendremos que añadir una función de loss más y lo haremos… con estilo.

Hablando con estilo

Como se ha explicado más arriba, el lenguaje debe ser creado espontáneamente y sin interacción humana, y para ello la representación en forma de espectrograma nos puede ayudar. Como es evidente, no podemos forzar que la salida del encoder sea igual (píxel a píxel) a un espectrograma concreto ni a un grupo de estos puesto que estaríamos violando el segundo supuesto del problema (existiría en ese caso fuerte interacción humana). Necesitaremos entonces una función de loss menos intrusiva, que no busque diferencias por píxel sino algo más general. Por suerte, en 2015 se introdujo un tipo de loss idóneo para este caso de uso: la loss de estilo (Gatys et al.). Intuitivamente, esta loss se calcula haciendo pasar las imágenes por una red neuronal preentrenada (VGG) y comparando las representaciones intermedias de la imagen objetivo y la imagen generada. Los autores aplican esta idea para transferir el estilo de un cuadro a una foto, manteniendo intacta la idea subyacente de la foto original. Para quien esté interesado, matemáticamente tiene este aspecto con \( l \) representaciones intermedias:

\[ L_{estilo} = \sum_l w^lL_{estilo}^l, \] \[ L_{estilo}^l = \dfrac{1}{M^l} \sum_{ij} (G_{ij}^l(s) - G_{ij}^l(g))^2, \] donde \( G(s) \) y \( G(g) \) se refieren a la matriz de Gram de la imagen estilo y la imagen generada respectivamente. En esta loss se está calculando la correlación entre las características extraídas en cada capa de la red preentrenada. Para más información, creo que este artículo (en inglés) puede ser interesante.

Podemos utilizar la loss de estilo para inducir que la salida del encoder sea similar a los espectrogramas de referencia. Con ello presumiblemente conseguiremos que los sonidos se mantengan aleatorios pero nos recuerden a los del droide de las películas. No obstante, esta función no puede ser aplicada a encoder y decoder por igual. Puesto que solo el encoder participa en el proceso de creación del lenguaje, es el único que debe recibir feedback en ese aspecto. Sin embargo, la idea debe fluir a través de ambas redes, por lo que la Cross-Entropy loss se debe propagar por todo el sistema. Así, las funciones en cada caso resultan: \[ L_{decoder} = L_{CE} = - \sum_i^C t_i \log(s_i),\] \[ L_{encoder} = L_{CE} + \lambda L_{estilo} = - \sum_i^C t_i \log(s_i) + \lambda \sum_l w^l \dfrac{1}{M^l} \sum_{ij} (G_{ij}^l(s) - G_{ij}^l(g))^2\]

Y el sistema total queda como en la Figura 4:

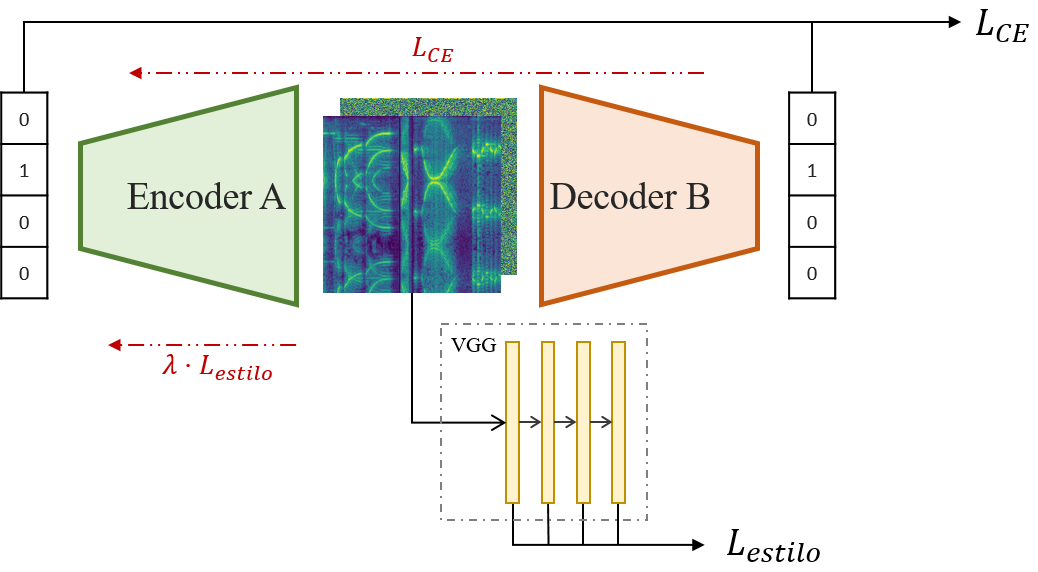Estructura con loss Figura 4: Propagación y cálculo de las funciones de _loss_ a través del sistema. En negro, propagación hacia delante. En rojo, propagación de las funciones de loss hacia atrás.

Hay que tener en cuenta que la simplicidad del mensaje que estamos transmitiendo puede suponer un problema a la hora de entrenar el encoder para que genere una representación adecuada, ya que podemos caer en una loss desbalanceada. Más adelante, dificultaremos la transmisión de mensajes añadiendo ruido a la representación intermedia, de forma que la salida del encoder no sea exactamente igual a la entrada del decoder, así conseguiremos perturbar el sistema y no conseguir \( L_{decoder} = L_{CE} = 0 \) tras unos pocos pasos de entrenamiento.

Solo restaría elegir una estrategia de entrenamiento. Como se ha descrito más arriba, cada sujeto está formado por dos redes con cometidos diferentes y cada comunicación enfrenta partes distintas de cada sujeto. Por lo tanto, con \( N \) sujetos tendremos \( 2N \) redes y \( N^2 \) formas de enfrentarlas (contando con que queremos que un sujeto pueda entenderse a sí mismo). Para entrenar a todos los sujetos a la vez y evitar que algunas redes adquieran más nivel que otras tendremos que seguir una estrategia escalonada, alternando los pasos de entrenamiento entre todas las combinaciones. Así, tanto el tiempo como la complejidad del entrenamiento crecen con \( \mathcal{O}(N^2) \).

Como creo que está quedando muy largo, mejor seguimos en otro post, por lo que cerramos aquí la primera parte de este artículo sobre cómo idear un sistema de redes neuronales del que pueda emerger un lenguaje común y cómo hacer que este lenguaje tenga la forma que queramos. En la segunda parte se explorarán los resultados y otras estrategias de entrenamiento en función de estos. Además, se incluirá una fuente de ruido para hacer el entrenamiento más robusto.

  1. Brown, Tom B., et al. Language Models Are Few-Shot Learners. May 2020, https://arxiv.org/abs/2005.14165.
  2. Shannon, C. E. “A Mathematical Theory of Communication.” Bell System Technical Journal, 1948, doi:10.1002/j.1538-7305.1948.tb01338.x.
  3. Neil, Carlson. “Physiology of Behavior.” IEEE Transactions on Information Theory, 2012.
  4. Bray, Adam, et al. Star Wars: Absolutely Everything You Need to Know. DK Children, 2015, p. 200.
  5. Krizhevsky, Alex, et al. “ImageNet Classification with Deep Convolutional Neural Networks.” Advances in Neural Information Processing Systems, 2012, doi:10.1061/(ASCE)GT.1943-5606.0001284.
  6. He, Kaiming, et al. “Deep Residual Learning for Image Recognition.” Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2016, doi:10.1109/CVPR.2016.90.
  7. Dot CSV. ¿Qué Es Una Red Neuronal Convolucional? Los OJOS De La Inteligencia Artificial - YouTube. 2020, https://www.youtube.com/watch?v=V8j1oENVz00.
  8. Stanford, Cs231n. CS231n Convolutional Neural Networks for Visual Recognition. https://cs231n.github.io/convolutional-networks/. Accessed December 21, 2020.
  9. Gómez, Raúl. Understanding Categorical Cross-Entropy Loss, Binary Cross-Entropy Loss, Softmax Loss, Logistic Loss, Focal Loss and All Those Confusing Names. May 2018, https://gombru.github.io/2018/05/23/cross_entropy_loss/.
  10. Gatys, Leon, et al. “A Neural Algorithm of Artistic Style.” Journal of Vision, 2015, doi:10.1167/16.12.326.

  1. En realidad el área de Wernicke y el área de Broca están conectadas por el fascículo arqueado (Neil). ↩

  2. Solo se muestra la magnitud en este espectrograma. Para calcularlo hay que tomar la transformada de Fourier de la señal, y eso lleva aparejada una fase que no se menciona aquí pero que es fundamental para hacer la transformada inversa después. ↩

  3. Esto aplica en modelos supervisados, en los que conocemos el valor que debería predecir el modelo para cada valor de entrada. Existen otros tipos de algoritmos (no supervisados, por ejemplo), en los que esto no se cumple y la función de loss adquiere otras formas. ↩